Convergence of Green function calculation
We check the convergence with \(N_\text{kpt}\) for the calculation of the vacancy Green function for FCC and HCP structures. In particular, we will look at:
The \(\mathbf{R}=0\) value,
The largest \(\mathbf{R}\) value in the calculation of a first neighbor thermodynamic interaction range,
The difference of the Green function value for (1) and (2),
with increasing k-point density.
[1]:
import sys
sys.path.extend(['../'])
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
%matplotlib inline
import onsager.crystal as crystal
import onsager.GFcalc as GFcalc
Create an FCC and HCP lattice.
[2]:
a0 = 1.
FCC, HCP = crystal.Crystal.FCC(a0, "fcc"), crystal.Crystal.HCP(a0, chemistry="hcp")
print(FCC)
print(HCP)
#Lattice:
a1 = [ 0. 0.5 0.5]
a2 = [ 0.5 0. 0.5]
a3 = [ 0.5 0.5 0. ]
#Basis:
(fcc) 0.0 = [ 0. 0. 0.]
#Lattice:
a1 = [ 0.5 -0.8660254 0. ]
a2 = [ 0.5 0.8660254 0. ]
a3 = [ 0. 0. 1.63299316]
#Basis:
(hcp) 0.0 = [ 0.33333333 0.66666667 0.25 ]
(hcp) 0.1 = [ 0.66666667 0.33333333 0.75 ]
We will put together our vectors for consideration:
Maximum \(\mathbf{R}\) for FCC = (400), or \(\mathbf{x}=2\hat j+2\hat k\).
Maximum \(\mathbf{R}\) for HCP = (440), or \(\mathbf{x}=4\hat i\), and (222), or \(\mathbf{x}=2\hat i + 2\sqrt{8/3}\hat k\).
and our sitelists and jumpnetworks.
[3]:
FCCR = np.array([0,2.,2.])
HCPR1, HCPR2 = np.array([4.,0.,0.]), np.array([2.,0.,2*np.sqrt(8/3)])
[4]:
FCCsite, FCCjn = FCC.sitelist(0), FCC.jumpnetwork(0, 0.75)
HCPsite, HCPjn = HCP.sitelist(0), HCP.jumpnetwork(0, 1.01)
We use \(N_\text{max}\) parameter, which controls the automated generation of k-points to iterate through successively denser k-point meshes.
[5]:
FCCdata = {pmaxerror:[] for pmaxerror in range(-16,0)}
print('kpt\tNkpt\tG(0)\tG(R)\tG diff')
for Nmax in range(1,13):
GFFCC = GFcalc.GFCrystalcalc(FCC, 0, FCCsite, FCCjn, Nmax=Nmax)
Nreduce, Nkpt, kpt = GFFCC.Nkpt, np.prod(GFFCC.kptgrid), GFFCC.kptgrid
for pmax in sorted(FCCdata.keys(), reverse=True):
GFFCC.SetRates(np.ones(1), np.zeros(1), np.ones(1)/12, np.zeros(1), 10**(pmax))
g0,gR = GFFCC(0,0,np.zeros(3)), GFFCC(0,0,FCCR)
FCCdata[pmax].append((Nkpt, g0, gR))
Nkpt,g0,gR = FCCdata[-8][-1] # print the 10^-8 values
print("{k[0]}x{k[1]}x{k[2]}\t".format(k=kpt) +
" {:5d} ({})\t{:.12f}\t{:.12f}\t{:.12f}".format(Nkpt, Nreduce,
g0, gR,g0-gR))
kpt Nkpt G(0) G(R) G diff
6x6x6 216 (16) -1.344901582401 -0.119888361621 -1.225013220779
10x10x10 1000 (48) -1.344674624975 -0.084566077531 -1.260108547444
14x14x14 2744 (106) -1.344663672542 -0.084541308263 -1.260122364278
18x18x18 5832 (200) -1.344661890661 -0.084539383601 -1.260122507060
22x22x22 10648 (337) -1.344661442418 -0.084538941204 -1.260122501213
26x26x26 17576 (528) -1.344661295591 -0.084538798573 -1.260122497018
30x30x30 27000 (778) -1.344661238153 -0.084538742761 -1.260122495392
34x34x34 39304 (1095) -1.344661212587 -0.084538717850 -1.260122494737
38x38x38 54872 (1491) -1.344661200055 -0.084538705591 -1.260122494464
42x42x42 74088 (1971) -1.344661193423 -0.084538699082 -1.260122494341
46x46x46 97336 (2545) -1.344661189691 -0.084538695410 -1.260122494281
50x50x50 125000 (3218) -1.344661187483 -0.084538693232 -1.260122494251
[6]:
HCPdata = []
print('kpt\tNkpt\tG(0)\tG(R1)\tG(R2)\tG(R1)-G(0)\tG(R2)-G0')
for Nmax in range(1,13):
GFHCP = GFcalc.GFCrystalcalc(HCP, 0, HCPsite, HCPjn, Nmax=Nmax)
GFHCP.SetRates(np.ones(1), np.zeros(1), np.ones(2)/12, np.zeros(2), 1e-8)
g0,gR1,gR2 = GFHCP(0,0,np.zeros(3)), GFHCP(0,0,HCPR1), GFHCP(0,0,HCPR2)
Nreduce, Nkpt, kpt = GFHCP.Nkpt, np.prod(GFHCP.kptgrid), GFHCP.kptgrid
HCPdata.append((Nkpt, g0, gR1, gR2))
print("{k[0]}x{k[1]}x{k[2]}\t".format(k=kpt) +
"{:5d} ({})\t{:.12f}\t{:.12f}\t{:.12f}\t{:.12f}\t{:.12f}".format(Nkpt, Nreduce,
g0, gR1, gR2,
g0-gR1, g0-gR2))
kpt Nkpt G(0) G(R1) G(R2) G(R1)-G(0) G(R2)-G0
6x6x4 144 (21) -1.367909503563 -0.192892722514 -0.131552967388 -1.175016781049 -1.236356536175
10x10x6 600 (56) -1.345034474341 -0.087913619020 -0.089866654871 -1.257120855321 -1.255167819470
16x16x8 2048 (150) -1.344668575390 -0.084546609595 -0.088212957806 -1.260121965795 -1.256455617584
20x20x12 4800 (308) -1.344662392185 -0.084539941251 -0.088166498574 -1.260122450934 -1.256495893611
26x26x14 9464 (560) -1.344661615456 -0.084539088966 -0.088165768509 -1.260122526490 -1.256495846946
30x30x16 14400 (819) -1.344661401027 -0.084538892419 -0.088165529659 -1.260122508608 -1.256495871368
36x36x20 25920 (1397) -1.344661260564 -0.084538764009 -0.088165374312 -1.260122496555 -1.256495886252
40x40x22 35200 (1848) -1.344661230214 -0.084538734661 -0.088165342770 -1.260122495553 -1.256495887444
46x46x24 50784 (2600) -1.344661210808 -0.084538715598 -0.088165322977 -1.260122495211 -1.256495887832
50x50x28 70000 (3510) -1.344661197817 -0.084538703416 -0.088165309065 -1.260122494400 -1.256495888752
56x56x30 94080 (4640) -1.344661192649 -0.084538698279 -0.088165303871 -1.260122494370 -1.256495888778
60x60x32 115200 (5627) -1.344661189980 -0.084538695678 -0.088165301128 -1.260122494302 -1.256495888852
First, look at the behavior of the error with \(p_\text{max}\)(error) parameter. The k-point integration error scales as \(N_\text{kpt}^{5/3}\), and we see the \(p_\text{max}\) error is approximately \(10^{-8}\).
[7]:
print('pmax\tGinf\talpha (Nkpt^-5/3 prefactor)')
Ginflist=[]
for pmax in sorted(FCCdata.keys(), reverse=True):
data = FCCdata[pmax]
Nk53 = np.array([N**(5/3) for (N,g0,gR) in data])
gval = np.array([g0 for (N,g0,gR) in data])
N10,N5 = np.average(Nk53*Nk53),np.average(Nk53)
g10,g5 = np.average(gval*Nk53*Nk53),np.average(gval*Nk53)
denom = N10-N5**2
Ginf,alpha = (g10-g5*N5)/denom, (g10*N5-g5*N10)/denom
Ginflist.append(Ginf)
print('{}\t{}\t{}'.format(pmax, Ginf, alpha))
pmax Ginf alpha (Nkpt^-5/3 prefactor)
-1 -1.3622362852792858 203.75410596197204
-2 -1.345225052792947 24.479334937158068
-3 -1.3446883432274557 3.322356166765774
-4 -1.3446627820660566 1.186618137589885
-5 -1.344661289561045 1.0554418717631806
-6 -1.3446611908160067 1.1378852023509276
-7 -1.3446611836353533 1.2547347330078438
-8 -1.344661182870995 1.403893171115624
-9 -1.344661182337601 1.6081890775249583
-10 -1.3446611814380371 1.8951451743398244
-11 -1.3446611800056545 2.291136009713601
-12 -1.344661177927421 2.8185182806123508
-13 -1.3446611751184294 3.4945030859983652
-14 -1.3446611715189616 4.331229854988949
-15 -1.3446611670905142 5.336529960337354
-16 -1.3446611618106175 6.514974709092111
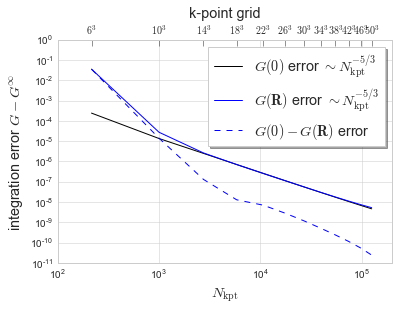
Plot the error in the Green function for FCC (at 0, maximum R, and difference between those GF). We extract the infinite value by fitting the error to \(N_{\mathrm{kpt}}^{-5/3}\), which empirically matches the numerical error.
[8]:
# plot the errors from pmax = 10^-8
data = FCCdata[-8]
Nk = np.array([N for (N,g0,gR) in data])
g0val = np.array([g0 for (N,g0,gR) in data])
gRval = np.array([gR for (N,g0,gR) in data])
gplot = []
Nk53 = np.array([N**(5/3) for (N,g0,gR) in data])
for gdata, start in zip((g0val, gRval, g0val-gRval), (0,1,2)):
N10,N5 = np.average(Nk53[start:]*Nk53[start:]),np.average(Nk53[start:])
denom = N10-N5**2
g10 = np.average(gdata[start:]*Nk53[start:]*Nk53[start:])
g5 = np.average(gdata[start:]*Nk53[start:])
Ginf,alpha = (g10-g5*N5)/denom, (g10*N5-g5*N10)/denom
gplot.append(np.abs(gdata-Ginf))
fig, ax1 = plt.subplots()
ax1.plot(Nk, gplot[0], 'k', label='$G(\mathbf{0})$ error $\sim N_{\mathrm{kpt}}^{-5/3}$')
ax1.plot(Nk, gplot[1], 'b', label='$G(\mathbf{R})$ error $\sim N_{\mathrm{kpt}}^{-5/3}$')
ax1.plot(Nk, gplot[2], 'b--', label='$G(\mathbf{0})-G(\mathbf{R})$ error')
ax1.set_xlim((1e2,2e5))
ax1.set_ylim((1e-11,1))
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_xlabel('$N_{\mathrm{kpt}}$', fontsize='x-large')
ax1.set_ylabel('integration error $G-G^\infty$', fontsize='x-large')
ax1.legend(bbox_to_anchor=(0.6,0.6,0.4,0.4), ncol=1,
shadow=True, frameon=True, fontsize='x-large')
ax2 = ax1.twiny()
ax2.set_xscale('log')
ax2.set_xlim(ax1.get_xlim())
ax2.set_xticks([n for n in Nk])
ax2.set_xticklabels(["${:.0f}^3$".format(n**(1/3)) for n in Nk])
ax2.set_xlabel('k-point grid', fontsize='x-large')
ax2.grid(False)
ax2.tick_params(axis='x', top='on', direction='in', length=6)
plt.show()
# plt.savefig('FCC-GFerror.pdf', transparent=True, format='pdf')
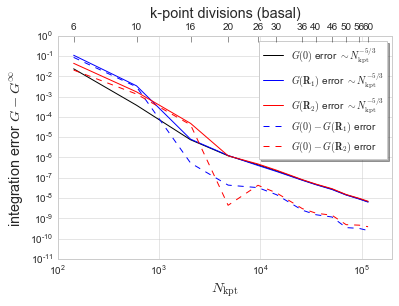
Plot the error in Green function for HCP.
[9]:
# plot the errors from pmax = 10^-8
data = HCPdata
Nk = np.array([N for (N,g0,gR1,gR2) in data])
g0val = np.array([g0 for (N,g0,gR1,gR2) in data])
gR1val = np.array([gR1 for (N,g0,gR1,gR2) in data])
gR2val = np.array([gR2 for (N,g0,gR1,gR2) in data])
gplot = []
Nk53 = np.array([N**(5/3) for (N,g0,gR1,gR2) in data])
for gdata, start in zip((g0val, gR1val, gR2val, g0val-gR1val, g0val-gR2val), (3,3,3,3,3)):
N10,N5 = np.average(Nk53[start:]*Nk53[start:]),np.average(Nk53[start:])
denom = N10-N5**2
g10 = np.average(gdata[start:]*Nk53[start:]*Nk53[start:])
g5 = np.average(gdata[start:]*Nk53[start:])
Ginf,alpha = (g10-g5*N5)/denom, (g10*N5-g5*N10)/denom
gplot.append(np.abs(gdata-Ginf))
fig, ax1 = plt.subplots()
ax1.plot(Nk, gplot[0], 'k', label='$G(\mathbf{0})$ error $\sim N_{\mathrm{kpt}}^{-5/3}$')
ax1.plot(Nk, gplot[1], 'b', label='$G(\mathbf{R}_1)$ error $\sim N_{\mathrm{kpt}}^{-5/3}$')
ax1.plot(Nk, gplot[2], 'r', label='$G(\mathbf{R}_2)$ error $\sim N_{\mathrm{kpt}}^{-5/3}$')
ax1.plot(Nk, gplot[3], 'b--', label='$G(\mathbf{0})-G(\mathbf{R}_1)$ error')
ax1.plot(Nk, gplot[4], 'r--', label='$G(\mathbf{0})-G(\mathbf{R}_2)$ error')
ax1.set_xlim((1e2,2e5))
ax1.set_ylim((1e-11,1))
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_xlabel('$N_{\mathrm{kpt}}$', fontsize='x-large')
ax1.set_ylabel('integration error $G-G^\infty$', fontsize='x-large')
ax1.legend(bbox_to_anchor=(0.6,0.6,0.4,0.4), ncol=1,
shadow=True, frameon=True, fontsize='medium')
ax2 = ax1.twiny()
ax2.set_xscale('log')
ax2.set_xlim(ax1.get_xlim())
ax2.set_xticks([n for n in Nk])
# ax2.set_xticklabels(["${:.0f}$".format((n*1.875)**(1/3)) for n in Nk])
ax2.set_xticklabels(['6','10','16','20','26','30','36','40','46','50','56','60'])
ax2.set_xlabel('k-point divisions (basal)', fontsize='x-large')
ax2.grid(False)
ax2.tick_params(axis='x', top='on', direction='in', length=6)
plt.show()
# plt.savefig('HCP-GFerror.pdf', transparent=True, format='pdf')